Диаграмма осадок судна носом и кормой

Одной из задач, возникающих в эксплуатации морского судна, является оперативная оценка его аварийной посадки и остойчивости при конкретной аварийной ситуации.
В частности, при посадке судна на мель или при получении пробоины капитану для принятия решения необходимо четко знать возможные последствия аварии. В зависимости от этого должны приниматься меры по организации борьбы по спасению судна или приниматься решение о необходимости экстренно покинуть его.
К сожалению, на судах полностью отсутствует какая-либо документация по оперативной оценке последствий его посадки на мель. В результате, не имея подробной информации в экстремальных ситуациях могут приниматься решения, приводящие к неблагоприятным последствиям.
В настоящей работе предлагаются достаточно простые методы для получения исходной информации при посадке судна на мель, и оценки возможности самостоятельного снятия с мели.
Для предварительных расчетов предлагается использовать хорошо знакомую каждому судоводителю диаграмму осадок носом и кормой (в дальнейшем называемую просто – диаграмма.)
Основные положения при работе с диаграммой.
Диаграмма осадок представляет собой набор кривых постоянных
значений осадок носом и кормой – dH и dK. Она индивидуальна для каждого судна и находится в «Информации об остойчивости для капитана». По осям координат диаграммы откладываются, как правило, следующие параметры:
- по оси абсцисс: дедвейт судна – D W или его водоизмещение D;
- по оси ординат: статический момент дедвейта (или водоизмещения) относительно плоскости мидельшпангоута – МХ. Он вычисляется в виде сумме всех составляющих статей нагрузок, входящих в дедвейт:
МХ = å mi xi (1)
где mi – статьи нагрузки судна
xi – продольная координата i статьи нагрузки.
Сами кривые на поле диаграммы могут быть построены или для осадок на носовых и кормовых перпендикулярах (НП и КП), или по маркам углублений данного судна.
Диаграмма удобна для оценки посадки судна при составлении каргоплана, для удифферентовки и при решении других задач.
При пользовании диаграммой необходимо помнить, что она построена без учета прогиба судна (т.е. стрелка прогиба в ней считается равной нулю: ƒ = 0).
Для работы с диаграммой необходимо найти положение рабочей точки, соответствующей нашему варианту загрузки судна. Положение рабочей точки на поле диаграммы однозначно задается ее координатами, т.е. величинами дедвейта (или водоизмещения) судна DW и его статического момента МХ. Эти значения определяются по формуле (1) при составлении таблицы весовой загрузки судна. Положение рабочей точки можно получить по фактическим значениям осадок носа и кормы судна.
На рис. 1 рабочая точка А имеет следующие значения координат:
абсцисса ХА = 5100 т; (ХА = DW),
ордината YА = 16000 тм; (YА = МХ).
как видно из рисунка через точку А проходят две линии dH = 4,0 м , dK = 5,0 м
эти и есть значения величины осадок носа и кормы судна.
Необходимо отметить очень важную особенность перемещения рабочей точки диаграммы при приеме (при снятии ) груза в конкретное помещение на судне. Так как продольная координата этого помещения – постоянная величина, то прием груза в него передвинет рабочую точку в строго заданном направлении. Например, если балласт берется в помещение на миделе (xб = 0), то рабочая точка будет перемещаться по горизонтали. Направление, по которому в общем случае передвинется точка А, определяется углом a, тангенс которого равен:
Зная величину xб для конкретного помещения, на диаграмме легко построить линию, на которой начнет перемещаться рабочая точка при приеме в него груза.
Вывод I.
Приложение силы в конкретной точке по длине судна вызывает перемещение рабочей точки на диаграмме в строго заданном направлении.
Выше было сказано, что диаграмма построена без учета прогиба ( перегиба ) судна, тем самым считается, что нанесенный на силуэт судна след ватерлинии является прямой линией (рис.2 ).
В этом случае, зная осадки в носу и корме – dн , dк , а также длину судна, можно довольно просто определить осадку в любом сечении судна, отстоящим от миделя на расстоянии х. Это легко выполнить графически, как показано на рис.2. Аналитически величина определяется по формуле:
Таким образом, каждая рабочая точка на диаграмме определяет для судна не только осадки носом и кормой, но и осадку в любом его сечении по длине судна.
Вывод II.
Каждой рабочей точке на диаграмме соответствует строго определенное положение судна относительно поверхности воды, и, следовательно, конкретная осадка в интересующем нас сечении.
Указанные два вывода позволяют подойти к решению задачи о посадке и снятии судна с мели и определения аварийной ватерлинии после получения пробоины.
Источник
Диаграмма
осадок носом и кормой (Пирсона),
именуемая также диаграммой дифферентов,
служит для оперативного решения различных
эксплуатационных задач при посадке
судна прямо и с дифферентом. Существует
несколько видов таких диаграмм. Рассмотрим
построение и использование одного
из наиболее удобных ее вариантов.
Наметим
на масштабе Бонжана ряд равноотстоящих
осадок носом и кормой, перекрывающих
весь желаемый диапазон посадок.
Фиксируя какое-либо значение
,
проведем через эту точку пучок ватерлиний,
проходящих через все намеченные точки
на кормовом перпендикуляре, и для каждой
из них найдем водоизмещение
V
и его статический момент относительно
миделя
.По
полученным значениям нанесем точки,
откладывая по вертикальной оси D = ρV, а
по горизонтальной — статический момент
Mx
= ρпри стандартном значении плотности ρ.
Полученные точки определят кривую, все
точки которой соответствуют посадкам
судна с одной и той же осадкой носомТн.
Поступая таким же образом со всеми
намеченными значениями Тн
и Tк,
получим сетку кривых постоянных
значений осадок носом и кормой,
определяющих посадку судна. Вместе
с тем, прямоугольные координаты D и Mx
точек определяют нагрузку судна, если
приближенно положить хg
≈ хс,
пренебрегая в первом из уравнений
равновесия (2.10) выражением
как
малой величиной при обычных дифферентах.
Таким образом, диаграмма дифферентов
(рис. 2.19) представляет собой наложенные
друг на друга две системы координат:
прямоугольную с осями D и Mx,
определяющую нагрузку судна, и
криволинейную с линиямиТн
и Tк,
определяющую
посадку судна.
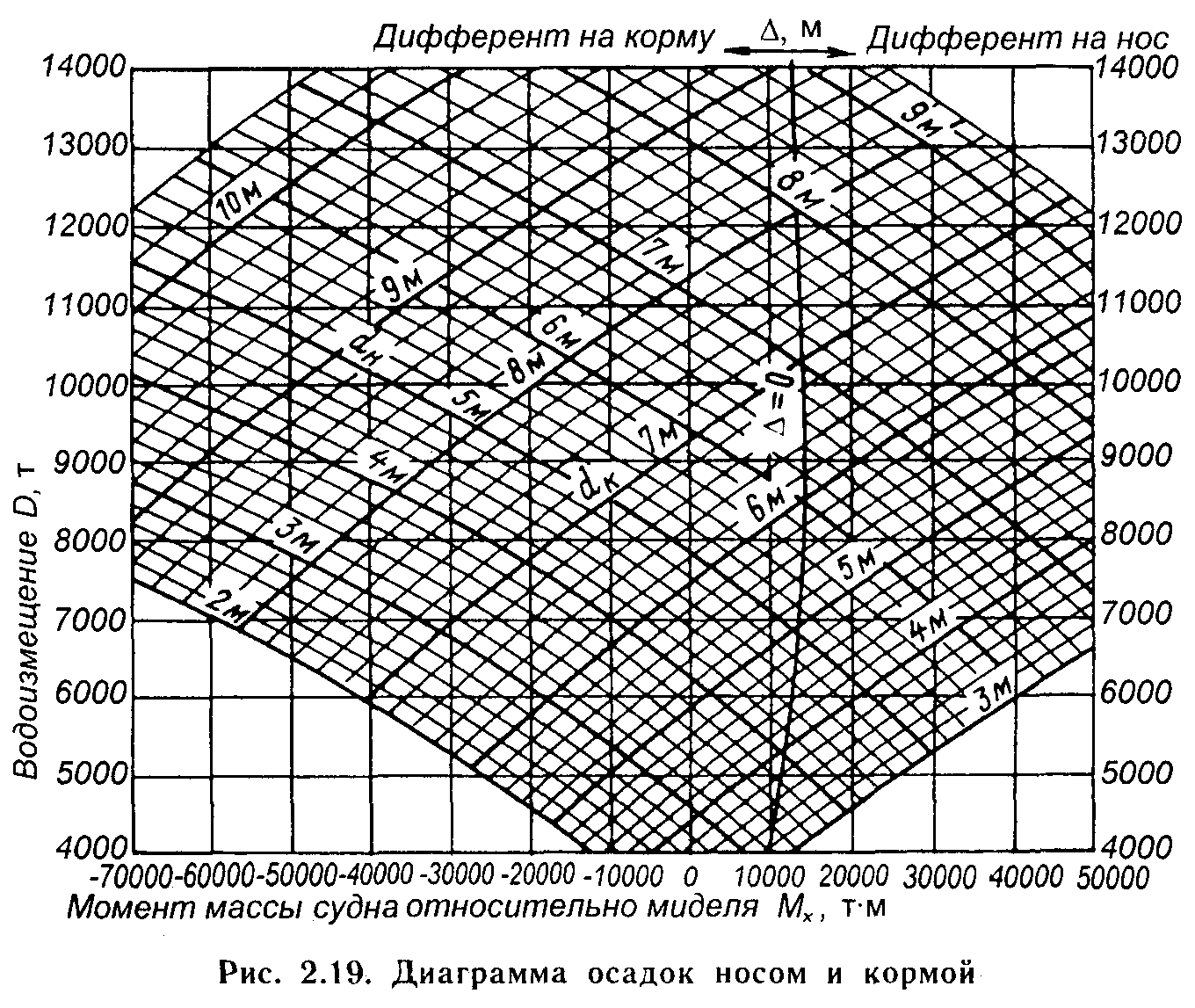
Рассмотрим
решение некоторых практических задач
с помощью диаграммы дифферентов.
По
составленному грузовому плану рассчитана
нагрузка судна: водоизмещение D и
статический момент водоизмещения
относительно миделя Mx
= Dхg.
Определить посадку судна. Откладывая
по вертикальной оси диаграммы
водоизмещение, а по горизонтальной —
момент, находим точку, изображающую
нагрузку судна. Пользуясь сеткой кривых
Тн
и Tк,
по найденной точке, при необходимости
интерполируя между кривыми, прочитываем
осадки носом и кормой для рассчитанного
состояния нагрузки. Обратная задача
(по заданной посадкеТн
и Tк
определить водоизмещениеD
и моментMx)
решается в обратном порядке: по Тн
и Тк
определяем точку на диаграмме, по которой
прочитываем D иMx
.
Диаграмма
дифферентов строится для стандартной
плотности воды ρ = 1,025 т/м3. Если плотность
забортной воды ρ1,
другая, то пользоваться диаграммой
следует по приведенным данным:

В
этом случае снятые с диаграммы по осадкам
Тн
и Тк
значения водоизмещения D и момента
Mx
будут приведенными, а их действительные
значения найдутся по выражениям:

Здесь
Dпр
и Mxпр
— значения снятые с диаграммы по осадкам
Тн
и Тк:
ρ1
— плотность заборной воды;
ρ
— плотность, воды, для которой построена
диаграмма.
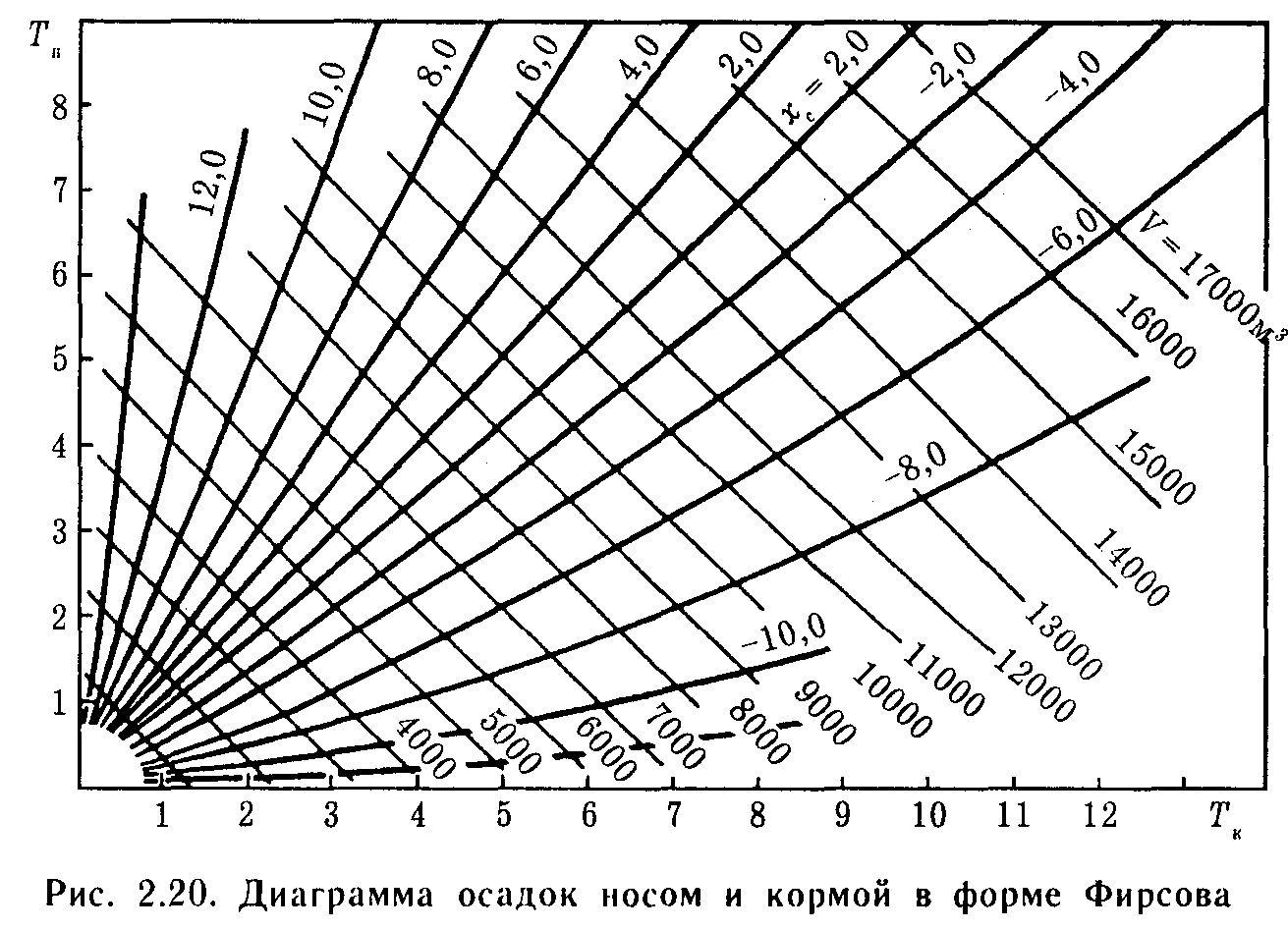
Другая
форма диаграммы осадок носом и кормой
представлена на рис. 2.20(ФИРСОВА).
Здесь осадки Тн
и Тк
отложены по вертикальной и горизонтальной
осям, а на поле диаграммы нанесены кривые
постоянных значений водоизмещения V и
абсциссы центра величины хс
. Пользуясь опять приближенным условием
равновесия хg
≈ хс
вместо точного условия (2.10), по определенным
после расчета таблицы нагрузки значениям
О и М находим

по
точке пересечения кривых V и хс
, соответствующих найденным значениям,
определяем осадки Тн
и Тк.
По этой диаграмме можно решать те же
задачи, что и по диаграмме рис. 2.19. Так,
после приема груза массой т с абсциссой
ЦТ. х будем иметь

и
по значениям
находим
точку на диаграмме рис. 2.20, по которой
прочитываем новую посадку Тн1
и Тк1.
Соседние файлы в предмете Теория и устройство судна
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Определение остойчивости.
Stability
Определение плавучести.
Floatability
Определение непотопляемости.
Определение общей и местной прочности.
Определение управляемости, устойчивости на курсе и поворотливости
Устойчивость на курсе – это способность судна сохранять направление прямолинейного движения.
Поворотливость – способность судна изменять направление движения и описывать траекторию заданной кривизны.
Определение ходкости.
Типы диаграмм дифферентов.
Types of trim diagram
Диаграмма осадок носом и кормой
Эта диаграмма именуемая также диаграммой дифферентов, служит для оперативного решения различных эксплуатационных задач при посадке судна прямо и с дифферентом. Существует несколько видов таких диаграмм. Рассмотрим построение и использование одного из наиболее удобных ее вариантов.
Наметим на масштабе Бонжана ряд равноотстоящих осадок носом и кормой, перекрывающих весь желаемый диапозон посадок. Фиксируя какое-либо значение Тн, проведем через точку на кормовом перпендикуляре, и для каждой из них найдем водоизмещение V и его статический момент относительно миделя Vx . По полученным значениям нанесем точки, откладывая по вертикальной оси D= V, а по горизонтльной – статический момент M = Vx при стандартном значении плотности . Полученные точки определяют кривую, все точки которой соответствуют посадкам судна с одной и той же осадкой носом Тн. Поступая таким же образом со всеми намеченными значениями Тн и Тк. Получим сетку кривых постоянных значений осадок носом и кормой, определяющих посадку судна. Вместе с тем, прямоуголные координаты D и М точек определяют нагрузку судна, если приближенно положить х х , пренебрегая в первом из уравнений равновесия (2.10) выражением (z – z )tg как малой величиной при обычных дифферентах. Т.о. диаграмма дифферентов ( рис. 2.19) представляет собой наложенные друг на друга две системы координат: прямоугольную с осями D и M , определяющую нагрузку судна, и криволинейную с линиями Тн и Тк, определяющую посадку судна.
Рассмотрим решение некоторых практических задач с помощью диаграммы дифферентов.
По составленному грузовому плану рассчитана нагрузка судна: водоизмещение D и статический момент водоизмещения относительно миделя M =D х . Определить посадку судна. Откладывая по вертикальной оси диаграммы водоизмещение, а по горизонтальной – момент, находим точку, изображающую нагрузку судна. Пользуясь сеткой кривых Тн и Тк, по найденной точке, при необходимости интерполируя между кривыми, прочитываем осадки носом и кормой для расчетного состояния нагрузки. Обратная задача ( по заданной посадке Тн и Тк определить водоизмещение D и момент M ) решается в обратном порядке : по Тн и Тк определяем точку на диаграмме, по которой прочитывается D и M .
Определить посадку судна после приема груза массой m с абсциссой центра тяжести x . Точку, изображающую первоначальную нагрузку или соответствующую первоначальную посадку, смещаем по вертикали вверх на величину m и по горизонтали на величину mx вправо, если она положительна, или влево,если она отрицательна. По полученной новой точке прочитываем новую осадку по кривым Тн и Тк.
Перенос груза по длине судна. Судно имеет посадку, определяемую осадками Тн и Тк Тн, т.е. с дифферентом на корму. Определить сколько балласта надо перекатать из ахтерпика в форпик, расстояние между которыми (измеренное между их центрами тяжести) равно l , чтобы посадить судно на ровный киль. По осадкам Тн и Тк находим на диаграмме изображающую точку. Так как при перекате балласта водоизмещение судна меняться не буде, изображающая точка будет перемещаться только по горизонтали и ее надо переместить до линии нулевого дифферента. Прочитав для этой точки момент М ’ , а также момент M для первоначальной точки, найдем момент M = M’ – M , который надо создать перемещением балласта, и определим массу балласта m = M /l.
Определить массу и абсциссу центра тяжести принятого груза, если до его приема осадки были Тн и Тк, а после приема стали Тн1 и Тк1. По осадкам находим водоизмещение D и момент М до приема груза и D и М после приема, откуда определяем массу груза m = D – D и абсциссу его центра тяжести
Требования и критерии начальной остойчивости Кодекса ИМО
Requirements and criteria regarding initial stability
Остойчивость при малых углах наклонения – начальная остойчивость.
Пара сил, образованная весом судна и силой поддержания, стремящаяся возвратить судно в первоначальное положение равновесия, называется восстанавливающей парой, а момент этой пары – восстанавливающим моментом Mθ.
Метацентрической высоты: поперечной метацентрической высотой называется возвышение поперечного метацентра над центром тяжести судна в начальном положении равновесия.
Метацентр – центр кривизны траектории по которой перемещается центр величиныв процессе наклонения.
Центр величины – точка приложения равнодействующих сил поддержания, действующих на судно (центр погруженной части корпуса)
Центр тяжести – точка приложения равнодействующих сил тяжести, действующих на судно.
Метацентрический радиус – определяется расстоянием от метацентра до центра величины.
Поперечная мегацентрическая высота (рис. 1) определяется расстоянием от центра тяжести (т. G), до поперечного метацентра (т. m), т.е. отрезком mG . Этот отрезок является постоянной величиной, т.к. и Ц.Т. ,и поперечный метацентр не изменяют своего положения при малых наклонениях. В связи с этим его удобно принимать в качестве критерия начальной остойчивости судна.
Если поперечный метацентр будет находиться выше центра тяжести судна, то поперечная метацентрическая высота считается положительной. Тогда условие остойчивости судна можно дать в следующей формулировке: Судно остойчиво, если его поперечная метацентрическая высота положительна. Чтобы установить, какими данными необходимо располагать для получения значения поперечной метацентрической высоты, обратимся к рис. 4, на котором показано относительное расположение центра величины С, центра тяжести G и поперечного метацентра m судна, имеющего положительную начальную поперечную остойчивость. Из рисунка видно, что поперечная метацентрическая высота h может быть определена по одной из следующих формул:
h = Zm – ZG, где Zm = r+Zc
М = P*l = D*g*h*sin – метацентрическая формула остойчивости
Требования и критерии Кодекса ИМО, регламентирующие характеристики ДСО.
Площадь под положительной частью ДСО:
А30°≥0,055 м*рад
А40°≥0,09 м*рад
А30-40≥0,03 м*рад
Максимальное плечо ДСО:
Lmaх≥0,25м для судов длинной ≤85
Lmaх≥0,2м для судов длинной ≥ 105м (максимальное восстанавливающие плечо)
Максимальный угол крена : Ө≥30°(Ө≥25)
Закат диаграммы: Өv≥60
Исправлення метац.высота h≥0.15m
Критерий погоды K=b/a≥1
Максимальное востанавливавающие плечо должно проходить под углом крена не менее чем 25°
Международный Кодекс по безопасной перевозке зерна насыпью. Требования к остойчивости.
International Code for the safe carriage of grain in bulk Stability Requirements
1. начальная метацентрическая высота, после коррекции для свободных поверхностных эффектов жидкостей в резервуарах, должна быть не менее 0,3 м.
2. Угол крена из-за смещения зерна не должен быть больше 12° или угол, при котором кромка палубы погружается, в зависимости от того, что меньше.
3.Аост≥0,075
INTERNATIONAL CODE
FOR THE SAFE CARRIAGE OF GRAIN IN BULK
RESOLUTION MSC.23(59)
(adopted on 23 May 1991)
Закон Фруда.
Конкретно закона нет! только такое
Число Фруда
Если помните, говоря о скорости судна, мы акцентировали ваше внимание на слове «относительная».
Дело в том, что скорость переходного режима каждого судна различна и напрямую зависит от его эффективной длины (обычно – длины по ватерлинии). Английский физик Уильям Фруд (1810–1879) подметил это, наблюдая за снующими по Темзе баржами (тогда – на лошадиной тяге). И не только подметил, но и вывел формулу, описывающую характер образуемых судном волн в зависимости от его длины и скорости:
Fr=v/√gl
Где:
v – скорость судна, м/с;
g – ускорение свободного падения, 9,81м/с2;
Lwl – длина судна по КВЛ, м;
Fr – число Фруда.
«Числа Фруда» описывают режим волнообразования для судов разного размера. Так, буксируя стократно уменьшенную модель в 10 раз медленнее реального судна, увидим такие же волны, как и у прототипа – только в масштабе 1:100.
Но что же числа Фруда означают практически? А вот что:
вплоть до Fr = 0,4 – водоизмещающий режим (при Fr = 0,4 судно начинает «карабкаться» на собственную носовую волну);
Fr = 0,5 – волновое сопротивление максимально; диапазон переходного режима Fr = 0,4…0,8;
при Fr = 1,0-1,2 – начало глиссирования, при котором судно поддерживается на поверхности как силой Архимеда, так и набирающей со скоростью удельный вес гидродинамической составляющей;
Fr = 1,5 – начало чистого глиссирования (судно поддерживается только гидродинамическими силами).
Водоизмещающее судно рассчитывают так, чтобы оно двигалось в диапазоне чисел Фруда до 0,2-0,3; для малых глиссирующих Fr≥2-3. Важная оговорка: граничные значения Фруда, отвечающие переходам одного режима в другой, весьма условны, так как зависят от формы погружённой части корпуса. Поэтому применять их для определения минимальной скорости воднолыжника или выхода судна на подводные крылья нельзя – на этот счёт есть формулы посложнее. Более того: для описания глиссирующего режима специалисты чаще оперируют не вышеописанным Fr (или FrL – по длине), а FrV (по водоизмещению), ибо в гидродинамическом режиме поддержания водоизмещение «важнее» длины…
Однако оставим тонкости профессионалам. А сами посчитаем абсолютные скорости входа и выхода из переходного режима для конкретно вашей лодки (по формуле выше). Лень считать – найдите «свою» пару цифр (в км/ч или узлах – как больше нравится) в таблице (напоминаю: для входа в неё нужна длина по КВЛ, а не габаритная!). Запомните их или нанесите метками на циферблат стрелочного лага (это нагляднее). А теперь главное: избегайте двигаться в диапазоне скоростей МЕЖДУ ними (т.е., в переходном режиме)
Уравнения качки судна
Motion equations
θm = α0 / (1 – σ2 / nθ2). Так как σ = 2π/τ, а nθ = 2π / Tθ,
то θm = α0 / (1 – Tθ2 / τ2) или θm/ α0 = 1 / (1 – Tθ2 / τ2) (1),
где θm – амплитуда качки;
α0 – наибольший угол волнового склона;
Tθ – период собственных колебаний судна;
τ – период волны.
Из уравнения следует, что по мере приближения периода волны τ к периоду собственных колебании Tθ относительная амплитуда вынужденных колебаний возрастает и при отсутствии сил сопротивления воды становится бесконечно большой (при τ – Tθ). Такое явление называется резонансом.
В действительности, резонанс, хотя и не приводит к возникновению бесконечно больших амплитуд, вызывает появление резонансных максимальных амплитуд. Из сравнения кривых, приведенных на рисунке видно, что влияние сопротивления воды на относительную амплитуду вынужденных колебаний существенно лишь в том случае, когда отношение периодов находится в интервале 0,70 ≤ Tθ / τ ≤ 1,3 ; вне этой области влияние сопротивления незначительно.
Рассматриваемый случай качки является наиболее опасным. Если судно не обладает достаточной динамической остойчивостыо, то резонанс может привести к потере остойчивости и к опрокидыванию судна. Именно поэтому при нормировании остойчивости морских судов оценивают углы, возникающие не только от действия динамически приложенного давления ветра, но и углы крена при бортовой качке, исходя из предположения, что судно находится на регулярном волнении в условиях резонанса при положении лагом к волне.
Определение остойчивости.
Stability
Определение плавучести.
Floatability
Определение непотопляемости.
Источник