На птицеферме употребляется два вида кормов

К группе задач о
смесях относят задачи по отысканию
наиболее дешевого набора из определенных
исходных материалов, обеспечивающих
получение смеси с заданными свойствами.
Иными словами, получаемые смеси должны
иметь в своем составе m различных
компонентов в определенных количествах,
а сами компоненты являются составными
частями n исходных материалов.

На птицеферме
употребляются два вида кормов – I и II. В
единице массы корма I содержатся единица
вещества A, единица вещества В и единица
вещества С. В единице массы корма II
содержатся четыре единицы вещества А,
две единицы вещества В и не содержится
вещество C. В дневной рацион каждой птицы
надо включить не менее единицы вещества
А, не менее четырех единиц вещества В и
не менее единицы вещества С. Цена единицы
массы корма I составляет 3 рубля, корма
II – 2 рубля.

Составьте ежедневный
рацион кормления птицы так, чтобы
обеспечить наиболее дешевый рацион.

Представим условие
задачи в таблице 2.2.

Таблица 2.2 – Исходные
данные задачи о смесях

Сформулируем
задачу линейного программирования.

Обозначим: x1
– количество корма I в дневном рационе
птицы, x2
– количество корма II в дневном рационе
птицы.

Формулировка ЗЛП:

3. Графический метод решения злп

Если система
ограничений задачи линейного
программирования представлена в виде
системы линейных неравенств с двумя
переменными, то такая задача может быть
решена геометрически. Таким образом,
данный метод решения ЗЛП имеет очень
узкие рамки применения.

Однако метод
представляет большой интерес с точки
зрения выработки наглядных представлений
о сущности задач линейного программирования.

Геометрический
(или графический) метод предполагает
последовательное выполнение ряда шагов.
Ниже представлен порядок решения задачи
линейного программирования на основе
ее геометрической интерпретации.

1. Сформулировать
ЗЛП.

2. Построить на
плоскости {х1,
х2}
прямые, уравнения которых получаются
в результате замены в ограничениях
знаков неравенств на знаки точных
равенств.

3. Найти полуплоскости,
определяемые каждым из ограничений
задачи.

4. Найти область
допустимых решений.

5. Построить прямую
c1x1
+ c2x2
= h, где h – любое положительное число,
желательно такое, чтобы проведенная
прямая проходила через многоугольник
решений.

6. Перемещать
найденную прямую параллельно самой
себе в направлении увеличения (при
поиске максимума) или уменьшения (при
поиске минимума) целевой функции. В
результате, либо отыщется точка, в
которой целевая функция принимает
максимальное (минимальное) значение,
либо будет установлена неограниченность
функции на множестве решений.

7. Определить
координаты точки максимума (минимума)
функции и вычислить значение функции
в этой точке.

Далее рассмотрим
пример решения ЗЛП графическим методом.
Для этого воспользуемся представленной
выше задачей о хоккейных клюшках и
шахматных наборах.

1. Выше уже приводилась
формулировка задачи, здесь нам остается
лишь повторить ее:

2. Теперь построим
прямые, соответствующие каждому из
функциональных ограничений задачи (см.
рисунок 1). Эти прямые обозначены на
рисунке (1), (2) и (3).

Рисунок 1.
Геометрическое решение ЗЛП

3. Штрихи на прямых
указывают полуплоскости, определяемые
ограничениями задачи.

4. Область допустимых
решений включает в себя точки, для
которых выполняются все ограничения
задачи. В нашем случае область представляет
собой пятиугольник (на рисунке обозначен
ABCDO и окрашен синим цветом).

5. Прямая,
соответствующая целевой функции, на
рисунке представлена пунктирной линией.

6. Прямую передвигаем
параллельно самой себе вверх (направление
указано стрелкой), поскольку именно при
движении в этом направлении значение
целевой функции увеличивается. Последней
точкой многоугольника решений, с которой
соприкоснется передвигаемая прямая,
прежде чем покинет его, является точка
C. Это и есть точка, соответствующая
оптимальному решению задачи.

7. Осталось вычислить
координаты точки С. Она является точкой
пересечения прямых (1) и (2). Решив совместно
уравнения этих прямых, найдем:
,.
Подставляя найденные величины в целевую
функцию, найдем ее значение в оптимальной
точке.

Таким образом, для
максимизации прибыли компании следует
ежедневно выпускать 24 клюшки и 4 шахматных
набора. Реализация такого плана обеспечит
ежедневную прибыль в размере $64.

2. Решение задачи
   линейного программирования в Excel
   (см. Презентацию)

7

Поиск
оптимальных решений в MSExcel.
Экономические приложения

Задача о смесях
(рационе, диете)

К группе задач о смесях
относят задачи по отысканию наиболее
дешевого набора из определенных исходных
материалов, обеспечивающих получение
смеси с заданными свойствами. Иными
словами, получаемые смеси должны иметь
в своем составе несколько различных
компонентов в определенных количествах,
а сами компоненты являются составными
частями нескольких исходных материалов.

Постановка
задачи

Предприятию
требуется изготовить некоторое количество
сплава, содержащего не менее 15 компонент
олова, 55 компонент цинка и 30 компонент
свинца. Требуемый сплав изготавливается
из трех исходных сплавов, в которых
содержатся вышеуказанные составляющие.
Данные о содержании олова, цинка и свинца
в исходных материалах приведены в
таблице, там же задана стоимость единицы
каждого сплава.

Следует
определить, какие из исходных сплавов
и в каких количествах нужно использовать
для получения требуемого сплава, чтобы
суммарные затраты на исходные сплавы
были минимальными.

Разработка
математической модели

Обозначим
через x1,
x2,
x3
количество единиц исходных сплавов
Сплава 1, Сплава 2 и Сплава 3 в требуемом
сплаве. Цель данной задачи – добиться
минимальных затрат на изготовление
требуемого сплава, поэтому общую
стоимость требуемого сплава можно
выразить в виде линейной функции

Принимая
во внимание данные приведенные в таблице
и условие, что требуемый сплав должен
содержать составляющих компонентов не
менее указанного, получаем систему
ограничений:

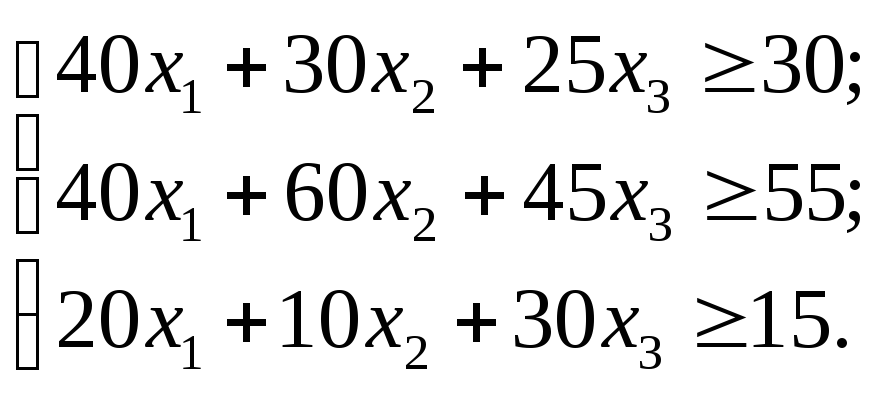
Если
Сплав 1 не используется в требуемом
сплаве, то
в
противном случае x1
больше 0. Аналогично имеем
и
,
т.е. должно выполняться условие
неотрицательности переменных.

Математическая
модель задачи выглядит следующим
образом.

Целевая
функция имеет вид:

ЦФ
представляет стоимость требуемого
сплава.

Ограничения
имеют вид:

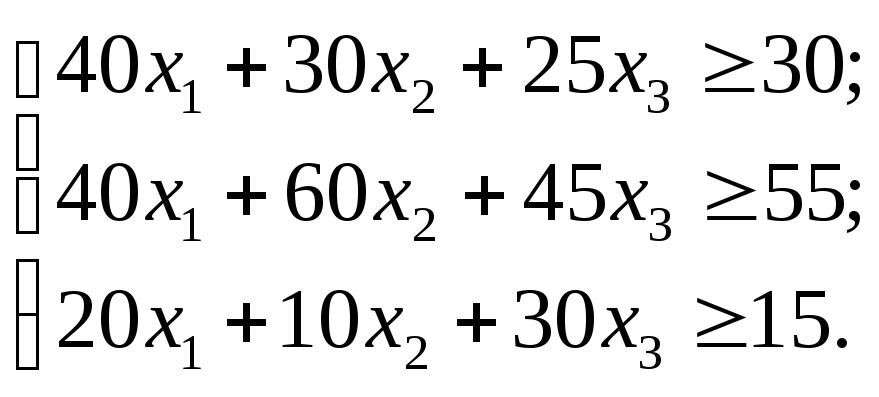
Ограничения
задачи представляют содержание
компонентов в сплаве, требуемый сплав
должен содержать компоненты в объемах,
не менее указанных.

Граничные
условия

представляют тот факт, количество
исходных сплавов не может быть
отрицательным.

Вид
электронной таблицы созданной для
решения задачи, представлен на рисунке.

Поиск
оптимального решения выполнить
самостоятельно.

Результат
поиска решения

Самостоятельная работа

1.
Для откорма животных употребляют два
корма: 1 и 2. Стоимость одного килограмма
корма 1 – 5 руб., корма 2 – 2 руб. В каждом
килограмме корма 1 содержится 5 ед.
витамина А, 2,5 ед. витамина В и 1 ед.
витамина С. В каждом килограмме корма
2 содержится 3 ед. витамина А, 3 ед. витамина
В и 1 ед. витамина С.

Какое
количество корма каждого вида необходимо
расходовать ежедневно, чтобы затраты
на откорм были минимальными, если
суточный рацион предусматривает не
менее 225 питательных единиц витамина
А, не менее 150 ед. витамина В и не менее
80 ед. витамина С?

2. Чтобы при откорме
животных весом 30-40 кг получить средний
привес 300-400 г, по нормам в дневном рационе
должны содержаться питательные вещества
в следующем количестве: кормовых единиц
– не менее 1,6 кг; переваримого протеина
– не менее 200 г, каротина – не менее 10
мг. При откорме используют ячмень, бобы
и сенную муку. Содержание питательных
веществ в 1 кг этих кормов и стоимости
1 кг корма приведены в
таблице.

Составить дневной
рацион, удовлетворяющий данной
питательности при минимальной стоимости.

3. На птицеферме
употребляется два вида кормов – I и II.
В единице веса корма I содержится единица
вещества А, единица вещества В и единица
вещества С. В единице веса корма II
содержатся четыре единицы вещества А,
две единицы вещества В и не содержится
вещество С. В дневной рацион каждой
птицы надо включить не менее единицы
вещества А, не менее четырех единиц
вещества В и не менее единицы вещества
С. Цена единицы веса корма I составляет
30 руб., корма II – 20 руб. Составить ежедневный
рацион кормления птицы таким образом,
чтобы обеспечить наиболее дешевый
рацион питания.

4. Для поддержания
нормальной жизнедеятельности человеку
ежедневно необходимо потреблять не
менее 118 г белков, 56 г жиров, 500 г углеводов,
8 г минеральных солей. Количество
питательных веществ, содержащихся в 1
кг каждого вида потребляемых продуктов,
а также цена 1 кг каждого из этих продуктов
приведены в следующей таблице:

Составить дневной
рацион, содержащий не менее суточной
нормы потребности человека в необходимых
питательных веществах при минимальной
общей стоимости потребляемых продуктов.

5. Фирма выпускает два
набора удобрений для газонов: обыч­ный
и улучшенный. В обычный набор входит 3
кг азотных, 4 кг фосфорных и 1 кг калийных
удобрений, а в улучшен­ный – 2 кг
азотных, 6 кг фосфорных и 3 кг калийных
удоб­рений. Известно, что для газона
требуется, по меньшей мере, 10 кг азотных,
20 кгфосфорных и 7 кг калий­ных
удобрений. Обычный набор стоит 3 д.ед.,
а улучшен­ный – 4 д.ед. Какие и сколько
наборов удобрений нужно ку­пить, чтобы
обеспечить эффективное питание почвы
и мини­мизировать стоимость?

6. Для откорма животных
в хозяйстве употребляют два вида кормов:
N1, N2, стоимость корма N1 – 500 ден.ед./кг,
корма N2 – 300 ден.ед./кг. Корм N1 содержит
5 ед/кг вещества А, 4 ед/кг вещества В, 2
ед/кг вещества С, корм N2 содержит
соответственно 6, 5, 3 ед/кг этих веществ.
Ежедневно может быть расходовано до 4
кг кормов каждого вида. Какое количество
корма каждого вида необходимо расходовать
ежедневно, чтобы затраты на откорм были
минимальными, если суточный рацион
должен содержать вещества А – не более
40 ед., вещества В – не менее 16 ед., вещества
С – не менее 17 ед.

7. Для кормления телят
фермер располагает двумя видами кормов:
комбикорм и ячмень молотый. Один килограмм
комбикорма дает 300 г привеса, ячменя
молотого – 100 г привеса. Комбикорм
содержит 20% сухого вещества, 2% протеина,
1% кальция, ячмень молотый – 50% сухого
вещества, 1% протеина, 2% кальция. Исходя
из максимального привеса, рассчитать
оптимальный суточный рацион из этих
двух видов кормов, если в нем (по норме)
должно содержаться не более 1 кг сухого
вещества, не менее 60 г протеина и не
менее 20 г кальция.

8. Современному
культурному фермеру Иванову (бывший
предсе­датель колхоза “Серпом по
молоту”) необходимо внести минераль­ные
удобрения под новую для него сельхозкультуру.
По новым реко­мендациям под эту
культуру в расчете на один гектар надо
вносить 10 кг азота, 8 кг фосфора и 5 кг
калия. На рынке имеется четыре вида
подходящих удобрений разных производителей.
Содержание необхо­димых элементов в
килограммах и цена в расчете на 1 тонну
для этих видов удобрения показаны в
следующей таблице.

Допустим, фермер Иванов
просит Вас как крупного специалиста по
принятию решений подсчитать, сколько
ему нужно купить удобре­ния каждого
типа и в каких пропорциях их смешивать,
чтобы было подешевле и чтобы содержание
необходимых элементов в смеси было не
меньше, чем советуют ученые. Всего Иванов
планирует внести эти удобрения на 90
гектаров.

5

КИТ, ЭКФАК, НИСПО, 2 КУРС,
ЗАОЧНОЕ